DAA


Merge Sort
Merge sort merupakan algoritma pengurutan dalam ilmu komputer yang dirancang untuk memenuhi kebutuhan pengurutan atas suatu rangkaian data yang tidak memungkinkan untuk ditampung dalam memori komputer karena jumlahnya yang terlalu besar.
Algoritma

Prinsip utama yang diimplementasikan pada algoritma merge-sort seringkali disebut sebagai pecah-belah dan taklukkan (bahasa Inggris: divide and conquer). Cara kerja algoritma merge sort adalah membagi larik data yang diberikan menjadi dua bagian yang lebih kecil. Kedua larik yang baru tersebut kemudian akan diurutkan secara terpisah. Setelah kedua buah list tersusun, maka akan dibentuk larik baru sebagai hasil penggabungan dari dua buah larik sebelumnya. Menurut keefektifannya, alogaritma ini bekerja dengan tingkat keefektifan O(nlog(n)). Dalam bentuk pseudocode sederhana algoritma ini dapat dijabarkan sebagai berikut:



# Original data is on the input tape; the other tapes are blank
 function merge_sort(input_tape, output_tape, scratch_tape_C, scratch_tape_D)
     while any records remain on the input_tape
         while any records remain on the input_tape
             merge( input_tape, output_tape, scratch_tape_C)
             merge( input_tape, output_tape, scratch_tape_D)
         while any records remain on C or D
             merge( scratch_tape_C, scratch_tape_D, output_tape)
             merge( scratch_tape_C, scratch_tape_D, input_tape)

 # take the next sorted chunk from the input tapes, and merge into the single given output_tape.
 # tapes are scanned linearly.
 # tape[next] gives the record currently under the read head of that tape.
 # tape[current] gives the record previously under the read head of that tape.
 # (Generally both tape[current] and tape[previous] are buffered in RAM ...)
 function merge(left[], right[], output_tape[])
     do
        if left[current] ≤ right[current]
            append left[current] to output_tape
            read next record from left tape
        else
            append right[current] to output_tape
            read next record from right tape
    while left[current] < left[next] and right[current] < right[next]
    if left[current] < left[next]
        append current_left_record to output_tape
    if right[current] < right[next]
        append current_right_record to output_tape
    return
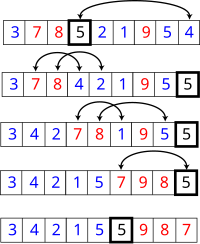
Contoh penerapan atas sebuah larik sebagai data sumber yang akan diurutkan {3, 9, 4, 1, 5, 2} adalah sebagai berikut:
  • Larik tersebut dibagi menjadi dua bagian, {3, 9, 4} dan {1, 5, 2}
  • Kedua larik kemudian diurutkan secara terpisah sehingga menjadi {3, 4, 9} dan {1, 2, 5}
  • Sebuah larik baru dibentuk yang sebagai penggabungan dari kedua larik tersebut {1}, sementara nilai-nilai dalam masing larik {3, 4, 9} dan {2, 5} (nilai 1 dalam elemen larik ke dua telah dipindahkan ke larik baru)
  • langkah berikutnya adalah penggabungan dari masing-masing larik ke dalam larik baru yang dibuat sebelumnya.
    • {1, 2} <-> {3, 4, 9} dan {5}
    • {1, 2, 3} <-> {4, 9} dan {5}
    • {1, 2, 3, 4} <-> {9} dan {5}
    • {1, 2, 3, 4, 5} <-> {9} dan {null}
    • {1, 2, 3, 4, 5, 9} <-> {null} dan {null}

Quick Sort

Quicksort adalah membagi dan menaklukkan algoritma . Quicksort pertama membagi besar daftar menjadi dua sub-daftar yang lebih kecil: elemen-elemen rendah dan elemen tinggi. Quicksort kemudian dapat secara rekursif semacam sub-daftar.
Langkah-langkahnya adalah:
  1. Pilih sebuah elemen, yang disebut poros , dari daftar.
  2. Menyusun ulang daftar sehingga semua elemen dengan nilai yang kurang dari pivot datang sebelum poros, sementara semua elemen dengan nilai lebih besar dari pivot datang setelah itu (nilai yang sama bisa jalan baik). Setelah partisi ini, poros pada posisi akhir. Ini disebut operasi partisi.
  3. Secara rekursif mengurutkan daftar sub-elemen yang lebih rendah dan daftar sub-elemen yang lebih besar.
Para kasus dasar dari rekursi adalah daftar ukuran nol atau satu, yang tidak pernah perlu diurutkan.

 Versi Sederhana

Di sederhana pseudocode , algoritma mungkin dinyatakan seperti ini:
 fungsi quicksort (array)
      var daftar kurang, lebih besar
      jika panjang (array) ≤ 1
          return array / / array nol atau satu elemen sudah diurutkan
      memilih dan menghapus poros poros nilai dari array
      untuk setiap x dalam array
          jika x ≤ poros kemudian tambahkan x kurang
          lain menambahkan x ke yang lebih besar
      kembali menggabungkan (quicksort (kurang), pivot, quicksort (lebih besar))
Perhatikan bahwa kita hanya meneliti unsur-unsur dengan membandingkan mereka dengan unsur-unsur lain. Hal ini membuat quicksort yangsemacam perbandingan . Versi ini juga merupakan semacam stabil (dengan asumsi bahwa "untuk setiap" metode mengambil elemen dalam urutan asli, dan poros yang dipilih adalah yang terakhir di antara mereka dengan nilai yang sama).
Kebenaran dari algoritma partisi didasarkan pada dua argumen berikut:
  • Pada setiap iterasi, semua elemen diproses sejauh ini dalam posisi yang diinginkan: sebelum poros jika kurang dari nilai pivot, setelah pivot jika lebih besar dari nilai pivot itu ( lingkaran invarian ).
  • Setiap iterasi daun satu elemen lebih sedikit untuk diproses ( varian lingkaran ).
Kebenaran dari algoritma secara keseluruhan dapat dibuktikan melalui induksi: untuk nol atau satu elemen, algoritma daun data tidak berubah, karena data set yang lebih besar menghasilkan gabungan dari dua bagian, elemen kurang dari pivot dan elemen-elemen lebih besar dari itu, sendiri diurutkan berdasarkan hipotesis rekursif.

 Dalam versi tempat

Kerugian dari versi sederhana di atas adalah bahwa ia memerlukan O (n) ruang penyimpanan tambahan, yang seburuk semacam bergabung .Alokasi memori tambahan yang diperlukan juga dapat secara drastis mempengaruhi kecepatan dan kinerja cache pada implementasi praktis. Ada versi yang lebih kompleks yang menggunakan di tempat algoritma partisi dan dapat mencapai jenis yang lengkap dengan menggunakan O (log n) ruang (tidak menghitung input) menggunakan rata-rata (untuk panggilan stack ):

Sebuah contoh quicksort.
 / / Kiri adalah index dari elemen paling kiri dari array
   / / Kanan adalah indeks dari elemen paling kanan dari array (inklusif)
   / / Jumlah elemen dalam subarray: kanan-kiri +1
   fungsi partisi (array, kiri, kanan, pivotIndex)
      pivotValue: = array [pivotIndex]
      Swap array [pivotIndex] dan array [kanan] / / Pindah poros untuk mengakhiri
      storeIndex: = kiri
      untuk i dari kiri ke kanan - 1 / / kiri ≤ i <kanan
          jika array [i] <pivotValue
              Swap array [i] dan array [storeIndex]
              storeIndex: = storeIndex + 1
      Swap array [storeIndex] dan array [kanan] / / Pindah poros ke tempat akhir
      kembali storeIndex
Ini adalah algoritma partisi di tempat. Ini partisi bagian dari array antara indeks kiri dan kanan, inklusif, dengan memindahkan semua unsur kurang dari atau sama denganarray[pivotIndex] ke awal subarray, meninggalkan semua elemen yang lebih besar mengikuti mereka. Dalam proses itu juga menemukan posisi akhir untuk elemen poros, yang kembali. Ini sementara elemen poros bergerak ke ujung subarray, sehingga tidak mendapatkan di jalan. Karena hanya menggunakan pertukaran, daftar akhir memiliki unsur-unsur yang sama dengan daftar asli. Perhatikan bahwa elemen dapat ditukar beberapa kali sebelum mencapai tempat akhir. Juga, dalam kasus duplikat poros dalam array masukan, mereka dapat tersebar di subarray kiri, mungkin dalam urutan acak. Ini tidak mewakili kegagalan partisi, seperti sortasi selanjutnya akan reposisi dan akhirnya "lem" mereka bersama-sama.

Di tempat partisi dalam aksi pada daftar kecil. Elemen kotak adalah elemen poros, elemen biru kurang atau sama, dan elemen merah besar.
Bentuk algoritma partisi tidak bentuk aslinya; beberapa variasi dapat ditemukan di berbagai buku pelajaran, seperti versi tidak memiliki storeIndex itu. Namun, bentuk ini mungkin paling mudah untuk memahami.
Setelah kami memiliki ini, menulis quicksort sendiri adalah mudah:
 fungsi quicksort (array, kiri, kanan)
      jika kanan> kiri / / subarray dari 0 atau 1 elemen sudah disortir
          pilih pivotIndex dalam kisaran kiri kanan ≤ ≤ pivotIndex  
              / / Lihat Pilihan poros untuk pilihan yang mungkin
          pivotNewIndex: = partisi (array, kiri, kanan, pivotIndex)
              / / Elemen pada pivotNewIndex sekarang pada posisi akhir
          quicksort (array, kiri, pivotNewIndex - 1)
              / / Secara rekursif mengurutkan unsur-unsur di kiri pivotNewIndex
          quicksort (array, pivotNewIndex + 1, kanan)  
              / / Secara rekursif mengurutkan elemen pada hak pivotNewIndex
Setiap panggilan rekursif untuk fungsi ini quicksort mengurangi ukuran array yang diurutkan oleh setidaknya satu elemen, karena dalam doa setiap elemen pada pivotNewIndex ditempatkan pada posisi akhir. Oleh karena itu, algoritma ini dijamin untuk mengakhiri setelah paling npanggilan rekursif. Namun, karena elemen menata ulang partisi dalam partisi, ini versi quicksort bukan semacam stabil.

  Implementasi isu

  Pilihan poros

Dalam versi awal dari quicksort, elemen paling kiri dari partisi sering akan dipilih sebagai elemen pivot. Sayangnya, hal ini menyebabkan perilaku terburuk pada array yang sudah diurutkan, yang merupakan yang agak umum digunakan-kasus. Masalahnya adalah mudah dipecahkan dengan memilih salah satu indeks acak untuk poros, memilih indeks tengah partisi atau (terutama untuk partisi lagi) memilih median dari elemen pertama, menengah dan terakhir dari partisi untuk poros (seperti yang direkomendasikan oleh R. Sedgewick ). [3] [4]
Memilih elemen poros juga rumit oleh adanya overflow integer . Jika indeks batas dari subarray yang diurutkan cukup besar, ekspresi naif untuk indeks menengah, (kiri + kanan) / 2,akan menyebabkan overflow dan memberikan indeks poros valid. Hal ini dapat diatasi dengan menggunakan, misalnya, kiri + (kanan-kiri) / 2 untuk indeks elemen tengah, pada biaya aritmatika lebih kompleks. Isu-isu serupa muncul dalam beberapa metode lain memilih elemen poros.

  Optimasi

Dua penting optimasi lainnya, juga disarankan oleh R. Sedgewick , seperti yang biasa diakui, dan banyak digunakan dalam praktek [5] [6] [7] adalah:
  • Untuk memastikan paling (log N) ruang O digunakan, recurse pertama ke setengah lebih kecil dari array, dan menggunakan panggilan ekor untuk recurse ke yang lain.
  • Gunakan insertion sort , yang memiliki faktor konstan yang lebih kecil dan dengan demikian lebih cepat pada array kecil, untuk doa pada array kecil seperti (yaitu di mana panjang kurang dari t ambang batas ditentukan secara eksperimental). Hal ini dapat diimplementasikan dengan meninggalkan array seperti disortir dan menjalankan satu penyisipan semacam lulus di akhir, karena insertion sort array menangani hampir diurutkan efisien. Sebuah insertion sort yang terpisah dari setiap segmen kecil karena mereka diidentifikasi menambahkan overhead untuk memulai dan menghentikan macam kecil banyak, namun, upaya menghindari membuang-buang membandingkan kunci melintasi batas-batas segmen banyak, yang akan kunci dalam rangka karena kerja dari proses quicksort . Hal ini juga meningkatkan penggunaan cache.

 > paralelisasi

Seperti menggabungkan semacam , quicksort juga dapat diparalelkan karena membagi-dan-menaklukkan-nya alam. Individu di tempat operasi partisi sulit untuk memparalelkan, tetapi sekali dibagi, bagian yang berbeda dari daftar dapat diurutkan secara paralel. Berikut ini adalah pendekatan langsung: Jika kita memiliki prosesor p, kita dapat membagi daftar elemen nke dalam sublists p dalam O (n) waktu rata-rata, kemudian mengurutkan masing-masing di \ Textstyle O \ left (\ frac {n} {p} \ log \ frac {n} {p} \ right) waktu rata-rata. Mengabaikan O (n) preprocessing dan waktu bergabung, ini adalah percepatan linier . Jika perpecahan itu buta, mengabaikan nilai-nilai, penggabungan naif biaya "O" ("n"). Jika partisi dibagi berdasarkan suksesi pivot, adalah sulit untuk memparalelkan dan naif biaya O (n). Mengingat O (log n) atau prosesor yang lebih, hanya O (n) waktu yang dibutuhkan secara keseluruhan, sedangkan sebagai pendekatan denganpercepatan linier akan mencapai O (log n) waktu untuk keseluruhan.
Satu keuntungan dari quicksort paralel sederhana atas lain semacam algoritma paralel adalah bahwa sinkronisasi tidak diperlukan, tetapi merugikan adalah bahwa pemilahan masih O (n) dan hanya speedup sublinear O (log n) dicapai. Sebuah thread baru dimulai sesegera subdaftar tersebut tersedia untuk itu untuk bekerja dan tidak berkomunikasi dengan benang lainnya. Ketika semua benang selesai, mengurutkan dilakukan.
Lain yang lebih canggih algoritma pengurutan paralel dapat mencapai batas-batas waktu yang lebih baik. [8] Sebagai contoh, pada tahun 1991 Powers Daud menggambarkan quicksort diparalelkan (dan terkait semacam radix ) yang dapat beroperasi dalam O (log n) waktu pada CRCW PRAM dengan n prosesor dengan melakukan partisi secara implisit. [9]

  Analisis formal

Dari deskripsi awal itu tidak jelas bahwa quicksort membutuhkan O (n log n) waktu rata-rata. Ini tidak sulit untuk melihat bahwa operasi partisi, yang hanya loop atas elemen dari array sekali, menggunakan O (n) waktu. Dalam versi yang melakukan penggabungan, operasi ini juga O (n).
Dalam kasus terbaik, setiap kali kita melakukan partisi kita membagi daftar menjadi dua bagian hampir sama. Ini berarti setiap panggilan rekursif proses daftar setengah ukuran.Akibatnya, kita dapat membuat hanya panggilan log n bersarang sebelum kita mencapai daftar ukuran 1. Ini berarti bahwa kedalaman pohon panggilan adalah log n. Tapi tidak ada dua panggilan pada tingkat yang sama dari proses pohon panggilan bagian yang sama dari daftar asli, dengan demikian, setiap tingkat panggilan hanya memerlukan O (n) semua bersama-sama (panggilan masing-masing memiliki beberapa overhead konstan, tapi karena ada hanya O (n) panggilan pada setiap tingkat, ini dimasukkan dalam faktor (n) O). Hasilnya adalah bahwa algoritma hanya menggunakan O (n log n) waktu.
Sebuah pendekatan alternatif adalah untuk mendirikan sebuah relasi rekurensi untuk faktor (n) T, waktu yang dibutuhkan untuk mengurutkan daftar ukuran n. Karena panggilan quicksort tunggal melibatkan O (n) bekerja faktor plus dua panggilan rekursif pada daftar ukuran n / 2 dalam kasus terbaik, hubungan akan menjadi:
T (n) = O (n) + 2T \ left (\ frac {n} {2} \ right).
Para Teorema Master memberitahu kita bahwa T (n) = O (n log n).
Bahkan, itu tidak perlu untuk membagi daftar ini justru, bahkan jika setiap pivot membagi elemen dengan 99% di satu sisi dan 1% di sisi lain (atau fraksi tetap lainnya), kedalaman panggilan masih terbatas pada 100 l o g n, sehingga waktu berjalan total masih O (n log n).
Dalam kasus terburuk, bagaimanapun, dua sublists memiliki ukuran 1 dan n - 1 (misalnya, jika array terdiri dari unsur yang sama dengan nilai), dan pohon panggilan menjadi sebuah rantai linier panggilan n bersarang. Panggilan ke i tidak O (n - i) bekerja, dan \ Textstyle \ sum_ {i = 0} ^ n (n-i) = O (n ^ 2) . Relasi rekursi adalah:
T (n) = O (n) + T (0) + T (n - 1) = O (n) + T (n - 1).
Ini adalah hubungan sama dengan insertion sort dan selection sort , dan memecahkan untuk T (n) = O (n 2). Pengetahuan yang diberikan yang dilakukan oleh perbandingan semacam itu, ada algoritma adaptif yang efektif untuk menghasilkan terburuk masukan untuk quicksort on-the-fly, terlepas dari strategi pemilihan poros. [10]

  Acak quicksort diharapkan kompleksitas

Acak quicksort memiliki properti yang diinginkan bahwa, untuk masukan apapun, hanya memerlukan O (n log n) diharapkan waktu (rata-rata lebih dari semua pilihan pivot). Tapi apa yang membuat pivot acak pilihan yang baik?
Misalkan kita menyortir daftar dan kemudian membaginya menjadi empat bagian. Dua bagian di tengah akan berisi pivot terbaik, masing-masing dari mereka adalah lebih besar dari setidaknya 25% dari unsur-unsur dan lebih kecil dari setidaknya 25% dari elemen. Jika kita secara konsisten dapat memilih elemen dari kedua bagian tengah, kita hanya harus membagi daftar paling 2log 2 n kali sebelum mencapai daftar ukuran 1, menghasilkan O (n log n) algoritma.
Sebuah pilihan acak hanya akan memilih dari bagian-bagian tengah separuh waktu. Namun, hal ini cukup baik. Bayangkan bahwa Anda membalik koin berulang-ulang sampai Anda mendapatkan kepala k. Meskipun ini bisa memakan waktu yang lama, rata-rata hanya 2 k membalik diperlukan, dan kesempatan bahwa Anda tidak akan mendapatkan kepala k setelah100 k membalik sangat mustahil. Dengan argumen yang sama, rekursi quicksort akan berakhir rata-rata pada kedalaman panggilan hanya 2 (2log 2 n). Tapi jika panggilan kedalaman rata-rata adalah O (log n), dan setiap tingkat proses panggilan pohon di n elemen yang paling, jumlah total kerja yang dilakukan rata-rata adalah produk, O (n log n). Perhatikan bahwa algoritma tidak harus memverifikasi bahwa poros ini di babak tengah - jika kita memukul setiap fraksi konstan dari kali, itu sudah cukup bagi kompleksitas yang diinginkan.
Garis besar bukti formal kompleksitas (n log n) waktu O diharapkan berikut. Asumsikan bahwa ada duplikasi tidak sebagai duplikat bisa ditangani dengan waktu linier pra-dan pasca-pengolahan, atau dianggap kasus lebih mudah daripada dianalisis. Memilih pivot, seragam secara acak dari 0 sampai n -1, kemudian setara dengan memilih ukuran satu partisi khusus, seragam secara acak dari 0 sampai n -1. Dengan pengamatan ini, kelanjutan bukti adalah analog dengan yang diberikan dalam bagian rata-rata kompleksitas .

  Rata-rata kompleksitas

Bahkan jika pivot tidak dipilih secara acak, quicksort masih membutuhkan hanya O (n log n) waktu rata-rata atas semua kemungkinan permutasi input. Karena rata-rata ini hanyalah jumlah waktu atas semua permutasi dari input dibagi dengan n faktorial, itu setara dengan memilih permutasi acak input. Ketika kita melakukan ini, pilihan poros dasarnya acak, menyebabkan algoritma dengan waktu berjalan sama seperti quicksort acak.
Lebih tepatnya, rata-rata jumlah perbandingan atas semua permutasi dari urutan input dapat diperkirakan secara akurat dengan memecahkan relasi rekurensi:
C (n) = n - 1 + \ frac {1} {n} \ sum_ {i = 0} ^ {n-1} (C (i) + C (ni-1)) = 2n \ ln n = 1,39 n \ log_2 n.
Di sini, n - 1 adalah jumlah perbandingan partisi menggunakan. Karena poros sama cenderung jatuh di mana saja dalam urutan daftar diurutkan, jumlah tersebut rata-rata atas segala kemungkinan perpecahan.
Ini berarti bahwa rata-rata, quicksort melakukan hanya sekitar 39% lebih buruk dari jumlah ideal perbandingan, yang merupakan kasus terbaik. Dalam hal ini lebih dekat dengan kasus terbaik dari kasus terburuk. Ini rata-rata runtime cepat adalah alasan lain untuk dominasi praktis quicksort atas algoritma pengurutan lain.

  Ruang kompleksitas

Ruang yang digunakan oleh quicksort tergantung pada versi yang digunakan.
Quicksort memiliki kompleksitas ruang O (log n), bahkan dalam kasus terburuk, ketika hati-hati diterapkan memastikan dua sifat berikut:
  • di tempat partisi yang digunakan. Hal ini memerlukan O (1) ruang.
  • Setelah selesai mempartisi, partisi dengan unsur paling sedikit adalah (secara rekursif) diurutkan pertama, membutuhkan paling (log n) ruang O. Kemudian partisi lain diurutkan menggunakan rekursi ekor atau iterasi, yang tidak menambah panggilan stack. Ide ini, seperti dibahas di atas, digambarkan oleh R. Sedgewick . [3] [4]
Versi quicksort dengan di tempat partisi hanya menggunakan ruang tambahan yang konstan sebelum melakukan panggilan rekursif. Namun, jika telah membuat O (log n) panggilan rekursif bersarang, perlu menyimpan sejumlah konstan informasi dari masing-masing. Sejak kasus terbaik membuat paling (log n) O panggilan rekursif bersarang, menggunakan O (log n)ruang. Kasus terburuk membuat O (n) panggilan rekursif bersarang, dan sehingga kebutuhan O (n) ruang; versi perbaikan Sedgewick dengan menggunakan rekursi ekor membutuhkan O(log n) ruang dalam kasus terburuk.
Kami eliding detail kecil di sini, namun. Jika kita mempertimbangkan memilah daftar sewenang-wenang yang besar, kita harus ingat bahwa variabel kita seperti kiri dan kanan tidak bisa lagi dianggap untuk menempati ruang yang konstan, melainkan membutuhkan O (log n) bit untuk indeks ke daftar item n. Karena kita memiliki variabel seperti ini dalam setiap stack frame, dalam kenyataannya quicksort memerlukan O ((log n) 2) bit ruang dalam kasus terbaik dan rata-rata dan O (n log n) ruang dalam kasus terburuk. Ini tidak terlalu buruk, meskipun, karena jika daftar berisi sebagian besar elemen yang berbeda, daftar itu sendiri juga akan menempati O (n log n) bit ruang.
Versi tidak-di-tempat quicksort menggunakan O (n) ruang bahkan sebelum membuat panggilan rekursif. Dalam kasus terbaik ruang yang masih terbatas pada O (n), karena setiap tingkat rekursi menggunakan setengah sebagai ruang sebanyak yang terakhir, dan
\ Sum_ {i = 0} ^ {\ infty} \ frac {n} {2 ^ i} = 2n.
Kasus terburuk adalah suram, membutuhkan
\ Sum_ {i = 0} ^ n (n-i +1) = O (n ^ 2)
ruang, jauh lebih banyak daripada daftar sendiri. Jika elemen list tidak sendiri ukuran konstan, masalah tumbuh bahkan lebih besar, misalnya, jika sebagian besar elemen list yang berbeda, masing-masing akan membutuhkan sekitar O (log n) bit, yang mengarah ke kasus terbaik O (n log n ) dan kasus terburuk O (n 2 log n) kebutuhan ruang.

 Seleksi berbasis pivoting

Sebuah algoritma seleksi memilih tanggal k terkecil dari daftar nomor, ini adalah masalah mudah secara umum dari penyortiran. Salah satu algoritma seleksi yang sederhana namun efektif bekerja hampir dengan cara yang sama seperti quicksort, kecuali bahwa alih-alih membuat panggilan rekursif pada kedua sublists, hanya membuat panggilan ekor rekursif tunggal pada subdaftar yang berisi elemen yang diinginkan. Ini perubahan kecil menurunkan kompleksitas rata-rata linier atau O (n) waktu, dan membuat suatu algoritma di tempat . Sebuah variasi pada algoritma ini membawa waktu terburuk turun ke O (n) (lihat algoritma seleksi untuk informasi lebih lanjut).
Sebaliknya, sekali kita tahu kasus terburuk O (n) algoritma seleksi tersedia, kita dapat menggunakannya untuk menemukan poros yang ideal (median) di setiap langkah dari quicksort, memproduksi varian dengan kasus terburuk O (n log n) waktu berjalan. Pada implementasi praktis, bagaimanapun, varian ini jauh lebih lambat pada rata-rata.
Varian lain adalah untuk memilih Median median sebagai elemen poros bukan median sendiri untuk partisi elemen. Sementara mempertahankan kompleksitas asimtotik waktu berjalan optimal O (n log n) (dengan mencegah partisi kasus terburuk), juga jauh lebih cepat daripada varian yang memilih median sebagai pivot.

 Varian

Ada tiga varian yang terkenal quicksort:
  • Seimbang quicksort: memilih kemungkinan untuk mewakili poros tengah nilai-nilai yang akan diurutkan, kemudian ikuti algoritma quicksort biasa.
  • Eksternal quicksort: Sama seperti quicksort biasa kecuali poros digantikan oleh buffer. Pertama, baca M / 2 elemen pertama dan terakhir ke buffer dan menyortir mereka. Baca elemen berikutnya dari awal atau akhir untuk menyeimbangkan menulis. Jika elemen berikutnya kurang dari yang paling buffer, menulis ke ruang yang tersedia di awal. Jika lebih besar dari yang terbesar, menulis sampai akhir. Jika tidak menulis terbesar atau paling buffer, dan menempatkan elemen berikutnya di dalam buffer. Jauhkan maksimum lebih rendah dan tombol atas minimal ditulis untuk menghindari beralih elemen tengah yang dalam rangka. Setelah selesai, menulis buffer. Secara rekursif semacam partisi yang lebih kecil, dan loop untuk mengurutkan partisi yang tersisa.
  • Tiga-cara radix quicksort (juga disebut multikey quicksort): adalah kombinasi dari semacam radix dan quicksort. Pilih sebuah elemen dari array (poros) dan mempertimbangkan karakter pertama (kunci) dari string (multikey). Partisi elemen yang tersisa menjadi tiga kelompok: mereka yang sesuai karakter kurang dari, sama dengan, dan lebih besar dari karakter poros itu. Rekursif, sort "kurang dari" dan "lebih besar dari" partisi pada karakter yang sama. Rekursif, sort "sama dengan" partisi dengan karakter berikutnya (kunci).

 Perbandingan dengan algoritma pengurutan lain

Quicksort adalah versi ruang-dioptimalkan dari semacam pohon biner . Alih-alih memasukkan item secara berurutan menjadi pohon eksplisit, quicksort mengatur mereka secara bersamaan menjadi sebuah pohon yang tersirat oleh panggilan rekursif. Algoritma membuat persis perbandingan yang sama, tetapi dalam urutan yang berbeda.
Pesaing paling langsung dari quicksort adalah heapsort . Heapsort terburuk-kasus berjalan waktu selalu O (n log n). Tapi, heapsort diasumsikan rata-rata agak lebih lambat dari quicksort. Ini masih diperdebatkan dan dalam penelitian, dengan beberapa publikasi yang menunjukkan sebaliknya. [11] [12] Dalam Quicksort tetap kemungkinan kasus terburuk kinerja kecuali dalam introsort varian, yang beralih ke heapsort ketika kasus buruk terdeteksi. Jika diketahui sebelumnya bahwa heapsort akan menjadi perlu, menggunakan secara langsung akan lebih cepat daripada menunggu introsort untuk beralih ke sana.
Quicksort juga bersaing dengan mergesort , lain algoritma rekursif semacam tetapi dengan manfaat terburuk O (n log n) waktu berjalan. Mergesort adalah semacam yang stabil , tidak seperti quicksort dan heapsort, dan dapat dengan mudah diadaptasi untuk beroperasi pada daftar terkait dan daftar yang sangat besar disimpan pada lambat-untuk-akses media sepertipenyimpanan disk atau penyimpanan jaringan terpasang . Meskipun quicksort dapat ditulis ke beroperasi pada daftar terkait, akan sering menderita dari pilihan poros miskin tanpa random access. Kerugian utama dari mergesort adalah bahwa, ketika beroperasi pada array, memerlukan O (n) ruang tambahan dalam kasus terbaik, sedangkan varian dari quicksort dengan di tempat partisi dan menggunakan rekursi ekor hanya O (log n) ruang. (Perhatikan bahwa ketika beroperasi pada daftar terkait, mergesort hanya membutuhkan sedikit jumlah konstan penyimpanan pembantu.)
Semacam ember dengan dua ember sangat mirip dengan quicksort, poros dalam hal ini secara efektif nilai di tengah rentang nilai, yang tidak baik pada rata-rata untuk input merata.

DFS
Order di mana node mendapatkan diperluas
Secara formal, DFS adalah sebuah pencarian uninformed yang berlangsung dengan memperluas simpul anak pertama dari pencarian pohon yang muncul dan dengan demikian akan lebih dalam dan lebih dalam sampai node tujuan ditemukan, atau sampai hits node yang tidak memiliki anak. Kemudian pencarian backtracks , kembali ke node yang paling terakhir ini belum selesai menjelajahi. Dalam pelaksanaan non-rekursif, semua node yang baru diperluas ditambahkan ke tumpukan untuk eksplorasi.
PROPERTY

Para waktu dan ruang analisis DFS berbeda menurut wilayah penerapannya. Dalam ilmu komputer teoritis, DFS biasanya digunakan untuk melintasi seluruh grafik, dan membutuhkan waktu O (| V | + | E |) , linear dalam ukuran grafik. Dalam aplikasi ini juga menggunakan ruang O (| V |) dalam kasus terburuk untuk menyimpan tumpukan vertex di jalan pencarian saat ini serta set simpul yang sudah dikunjungi. Jadi, dalam pengaturan ini, batas-batas waktu dan ruang adalah sama seperti untuk luas pertama pencarian dan pilihan yang kedua algoritma untuk menggunakan tergantung kurang pada kompleksitas dan lebih pada sifat-sifat yang berbeda dari orderings titik dua algoritma menghasilkan .
Untuk aplikasi DFS untuk mencari masalah dalam kecerdasan buatan , bagaimanapun, grafik yang akan dicari sering terlalu besar untuk mengunjungi secara keseluruhan atau bahkan tak terbatas, dan DFS mungkin menderita dari non-pemutusan kontrak kerja ketika panjang jalur di pohon pencarian tak terbatas. Oleh karena itu, pencarian hanya dilakukan dengan kedalaman terbatas, dan karena satu memori ketersediaan terbatas biasanya tidak menggunakan struktur data yang melacak himpunan semua simpul yang dikunjungi sebelumnya. Dalam kasus ini, waktu masih linier dalam jumlah vertex diperluas dan tepi (walaupun nomor ini tidak sama dengan ukuran keseluruhan grafik karena beberapa titik bisa dicari lebih dari sekali dan lain-lain tidak sama sekali) tapi ruang kompleksitas ini varian dari DFS hanya sebanding dengan batas kedalaman, jauh lebih kecil daripada ruang yang dibutuhkan untuk mencari sampai kedalaman yang sama dengan menggunakan lebar-pertama pencarian. Untuk aplikasi tersebut, DFS juga meminjamkan sendiri jauh lebih baik untuk heuristik metode memilih cabang yang tampak mungkin. Ketika batas kedalaman yang tepat tidak diketahui apriori, berulang memperdalam kedalaman-pertama pencarian DFS berlaku berulang-ulang dengan urutan batas meningkat; dalam modus kecerdasan buatan analisis, dengan branching factor lebih besar dari satu, berulang memperdalam meningkatkan waktu berjalan dengan hanya faktor konstan selama kasus di mana batas kedalaman yang benar dikenal karena pertumbuhan geometris dari jumlah node per tingkat.
CONTOH:

Untuk grafik berikut:
Graph.traversal.example.svg
pencarian mendalam-pertama kali memulai pada A, dengan asumsi bahwa tepi kiri dalam grafik yang ditampilkan adalah dipilih sebelum tepi kanan, dan dengan asumsi pencarian ingat node sebelumnya dikunjungi dan tidak akan mengulangi mereka (karena ini adalah grafik kecil), akan mengunjungi node dalam urutan sebagai berikut: A, B, D, F, E, C, G. tepi dilalui dalam bentuk pencarian pohon Trémaux , struktur dengan aplikasi penting dalam teori grafik .
Melakukan pencarian yang sama tanpa mengingat hasil node yang telah dikunjungi sebelumnya dalam mengunjungi node dalam urutan A, B, D, F, E, A, B, D, F, E, dll selamanya, terperangkap dalam A, B, D, F , E siklus dan tidak pernah mencapai C atau G.
Iteratif memperdalam adalah salah satu teknik untuk menghindari hal ini infinite loop dan akan mencapai semua node.

 Output pencarian depth-first



Hasil yang paling alami pencarian pertama kedalaman grafik (jika dianggap sebagai fungsi daripada prosedur ) adalah pohon rentangdari simpul yang dicapai selama pencarian. Berdasarkan pohon rentang, tepi grafik asli dapat dibagi menjadi tiga kelas: tepi maju(atau "penemuan tepi"), yang titik dari node dari pohon ke salah satu keturunannya, kembali tepi, titik mana dari node ke salah satu nenek moyang, dan lintas tepi, yang melakukan keduanya. Kadang-kadang pohon tepi, tepi yang termasuk ke dalam pohon rentang itu sendiri, diklasifikasikan secara terpisah dari tepi ke depan. Hal ini dapat ditunjukkan bahwa jika grafik asli berarah maka semua ujungnya adalah pohon tepi atau tepi kembali.

 orderings Vertex

Hal ini juga memungkinkan untuk menggunakan pencarian mendalam-pertama urutan linear simpul dari grafik asli (atau pohon). Ada tiga cara yang umum untuk melakukan hal ini:
  • Preordering adalah daftar simpul dalam urutan yang mereka pertama kali dikunjungi oleh algoritma pencarian mendalam-dulu. Ini adalah cara yang kompak dan alami menggambarkan kemajuan pencarian, seperti yang dilakukan sebelumnya dalam artikel ini. Sebuah preordering sebuah pohon ekspresi adalah ekspresi dalam notasi Polandia .
  • Sebuah postordering reverse kebalikan dari postordering, yaitu daftar simpul dalam urutan kebalikan dari kunjungan terakhir mereka. Saat mencari pohon, postordering reverse sama preordering, namun secara umum mereka berbeda ketika mencari grafik. Misalnya, ketika mencari grafik diarahkan

mulai dari simpul A, satu kunjungan node dalam urutan, untuk menghasilkan daftar baik ABDBACA, atau ACDCABA (tergantung pada apakah algoritma memilih untuk mengunjungi B atau C pertama). Perhatikan bahwa mengulangi kunjungan dalam bentuk mundur ke sebuah node, untuk memeriksa apakah itu masih belum dikunjungi tetangga, termasuk di sini (bahkan jika ditemukan memiliki tidak ada). Jadi preorderings mungkin adalah ABDC dan ACDB (order dengan terjadinya simpul paling kiri dalam daftar di atas), sedangkan postorderings sebaliknya yang mungkin ACBD dan ABCD (order dengan terjadinya simpul paling kanan dalam daftar di atas). Postordering sebaliknya menghasilkan pengurutan topologi dari setiap grafik asiklik diarahkan . Memesan ini juga berguna dalam analisis kontrol aliran seperti yang sering merupakan Linearisasi alami dari aliran kontrol. Grafik di atas mungkin mewakili aliran kontrol dalam sebuah fragmen kode seperti
 jika (A), {
        B
      } Else {
        C
      }
      D
dan adalah wajar untuk mempertimbangkan kode ini di urutan ABCD atau ACBD, tetapi tidak alami untuk menggunakan perintah ABDC atau ACD B.

  Pseudocode

Input: Sebuah grafik G dan simpul v dari G
Output: Sebuah pelabelan dari tepi dalam komponen terhubung dari v sebagai penemuan dan tepi tepi kembali
 1 prosedur DFS (G, v):
 2 label v sebagai dieksplorasi
 3 untuk semua e tepi di G.incidentEdges (v) melakukan
 4 jika e edge belum diselidiki kemudian
 5 w ← G.opposite (v, e)
 6 jika w adalah verteks belum diselidiki kemudian
 7 label e sebagai tepi penemuan
 8 rekursif panggilan DFS (G, w)
 9 lainnya 
 10 label e sebagai ujung belakang

  Algoritma menggunakan stack

  1. Dorong simpul akar ke tumpukan .
  2. Pop node dari stack dan memeriksanya.
    • Jika elemen yang dicari ditemukan di node ini, berhenti pencarian dan mengembalikan hasilnya.
    • Jika tidak mendorong semua penerusnya (node ​​anak) yang belum ditemukan ke stack.
  3. Jika stack kosong, setiap node di pohon telah diperiksa - berhenti mencari dan kembali "tidak ditemukan".
  4. Jika tumpukan tidak kosong, ulangi dari Langkah 2.
Catatan: Menggunakan antrian bukan stack akan mengubah algoritma ini menjadi pencarian luas-pertama .

 Aplikasi

Maze 30x20 DFS.ogv

Mirip dengan depth-first pencarian yang digunakan dalam menghasilkan labirin acak algoritma.
Algoritma yang menggunakan depth first pencarian sebagai sebuah blok bangunan meliputi:

BFS
Order di mana node mendapatkan diperluas

BFS adalah pencarian uninformed metode yang bertujuan untuk memperluas dan memeriksa semua node dari grafik atau kombinasi dari sekuen secara sistematis mencari melalui setiap solusi. Dengan kata lain, secara mendalam akan mencari seluruh grafik atau urutan tanpa mempertimbangkan tujuan sampai menemukannya. Ini tidak menggunakan heuristik algoritma.

Dari sudut pandang algoritma , semua node anak diperoleh dengan memperluas simpul ditambahkan ke FIFO (yaitu, Pertama Dalam, First Out) antrian .Dalam implementasi khas, node yang belum diperiksa untuk tetangga mereka ditempatkan dalam beberapa wadah (seperti antrian atau linked list ) yang disebut "terbuka" dan kemudian sekali diperiksa ditempatkan dalam wadah "tertutup".

Peta contoh dari Jerman dengan beberapa koneksi antara kota-kota

Pohon-luasnya pertama diperoleh saat menjalankan BFS pada peta yang diberikan dan mulai tahun Frankfurt

Animasi contoh pencarian luas-pertama

 Algoritma (informal)


  1. Enqueue simpul akar.
  2. Dequeue sebuah node dan memeriksanya.
    • Jika elemen yang dicari ditemukan di node ini, berhenti pencarian dan mengembalikan hasilnya.
    • Jika tidak ada pengganti enqueue (node ​​anak langsung) yang belum ditemukan.
  3. Jika antrian kosong, setiap node pada grafik telah diperiksa - berhenti mencari dan kembali "tidak ditemukan".
  4. Jika antrian tidak kosong, ulangi dari Langkah 2.
Catatan: Menggunakan tumpukan bukannya antrian akan mengubah algoritma ini menjadi pencarian mendalam-dulu .


Pseudocode

 1 Prosedur BFS (Grafik, sumber):
 2 membuat antrian Q
 3 enqueue sumber ke Q
 4 tandai sumber
 5 sedangkan Q tidak kosong:
 6 dequeue item dari Q ke v
 7 untuk setiap insiden e tepi pada v pada Grafik:
 8 membiarkan w ujung e
 9 jika w tidak ditandai:
 10 tanda w
 11 enqueue w ke Q


Fitur


Ruang kompleksitas

Karena semua node tingkat harus disimpan sampai anak mereka node dalam tingkat berikutnya telah dihasilkan, kompleksitas ruang adalah sebanding dengan jumlah node pada tingkat yang terdalam. Mengingat branching factor b dan grafik kedalaman d kompleksitas ruang asimtotik adalah jumlah node pada tingkat yang terdalam, O (b d). Ketika jumlah simpul dalam grafik dikenal sebelumnya, dan tambahan struktur data yang digunakan untuk menentukan simpul telah ditambahkan ke antrian, kompleksitas ruang juga dapat dinyatakan sebagaiO (| V |) dimana | V | adalah kardinalitas dari himpunan simpul. Dalam kasus terburuk grafik memiliki kedalaman 1 dan semua simpul harus disimpan. Karena eksponensial dalam kedalaman grafik, luas pertama pencarian sering tidak praktis untuk masalah-masalah besar pada sistem dengan ruang yang terbatas.


Kompleksitas Waktu

Karena dalam kasus terburuk luas pertama pencarian harus mempertimbangkan semua jalan ke semua node mungkin kompleksitas waktu dari luas pertama pencarian 1 + b + b ^ 2 + b ^ 3 + \ cdots + b ^ d yaitu O (b d). Kompleksitas waktu juga dapat dinyatakan sebagai O (| E | + | V |) karena setiap simpul dan tepi setiap akan dieksplorasi dalam kasus terburuk.


Kelengkapan

Pencarian Breadth-first selesai. Ini berarti bahwa jika ada solusi, luas pertama pencarian akan menemukan terlepas dari jenis grafik. Namun, jika grafik tidak terbatas dan tidak ada solusi luas pertama pencarian akan berbeda .


Bukti kelengkapan

Jika node tujuan dangkal adalah di beberapa kedalaman terbatas katakan d, luas pertama pencarian akhirnya akan menemukan setelah memperluas semua node dangkal (asalkan b branching factor adalah terbatas). [1]


optimalitas

Untuk unit-langkah biaya, luas pertama pencarian optimal. Secara umum luas pertama pencarian tidak optimal karena selalu mengembalikan hasilnya dengan tepi paling sedikit antara node awal dan node tujuan. Jika grafik adalah graf berbobot, dan karenanya memiliki biaya yang terkait dengan setiap langkah, sebuah tujuan berikutnya untuk memulai tidak harus menjadi tujuan termurah yang tersedia. Masalah ini dipecahkan dengan meningkatkan luas-pertama pencarian untuk seragam-biaya pencarian yang menganggap biaya jalan. Namun demikian, jika grafik tidak berbobot, dan karena itu semua biaya langkah yang sama, luas pertama pencarian akan menemukan solusi terdekat dan terbaik.

Bias terhadap node dari tingkat tinggi

Telah diamati secara empiris (dan analitis ditunjukkan untuk grafik acak) yang lengkap luas-pertama pencarian bias terhadap node tinggi derajat . Hal ini membuat luas pertama pencarian sampel dari grafik sangat sulit untuk menafsirkan. Sebagai contoh, sampel luas-pertama 1 juta node dalam Facebook (kurang dari 1% dari seluruh grafik) overestimates derajat rata-rata 240 simpul%. [2]


Aplikasi

Pencarian Breadth-first dapat digunakan untuk memecahkan banyak masalah dalam teori graf, misalnya:


komponen yang terhubung Mencari

Himpunan node dicapai oleh BFS (breadth-first search) membentuk komponen terhubung yang berisi node awal.


bipartiteness Pengujian

BFS dapat digunakan untuk menguji bipartiteness , dengan memulai pencarian pada setiap vertex dan memberikan label bolak-balik ke simpul yang dikunjungi selama pencarian.Artinya, memberi label 0 untuk titik awal, 1 untuk semua tetangga, tetangga 0 sampai mereka tetangga, dan seterusnya. Jika pada setiap langkah simpul memiliki (dikunjungi) tetangga dengan label yang sama seperti dirinya sendiri, maka grafik tidak bipartit. Jika pencarian berakhir tanpa terjadi situasi seperti itu, maka grafik adalah bipartit.

MINIMUM SPANNING TREE
Mengingat terhubung , grafik diarahkan , sebuah pohon rentang dari graf yang merupakan subgraf yang merupakan pohon dan menghubungkan semua simpul bersama-sama. Sebuah grafik tunggal dapat memiliki banyak pohon rentang yang berbeda. Kita juga dapat menetapkan berat badan untuk setiap sisi, yang merupakan angka yang mewakili bagaimana tidak menguntungkan itu, dan menggunakan ini untuk menetapkan berat badan ke spanning tree dengan menghitung jumlah bobot dari tepi dalam spanning tree. Sebuah pohon rentang minimum (MST) atau pohon rentang berat minimum kemudian pohon rentang dengan berat badan kurang dari atau sama dengan berat dari setiap pohon rentang lain. Lebih umum, setiap grafik diarahkan (tidak harus terhubung) memiliki hutan rentang minimum, yang merupakan gabungan dari pohon rentang minimum untuk perusahaan komponen yang terhubung .
Salah satu contoh akan menjadi TV kabel perusahaan kabel peletakan ke lingkungan baru. Jika dibatasi untuk mengubur kabel hanya di sepanjang jalan tertentu, maka akan ada grafik yang mewakili titik-titik dihubungkan oleh jalan tersebut. Beberapa dari mereka jalan mungkin lebih mahal, karena mereka lebih lama, atau memerlukan kabel yang akan dikubur lebih dalam, jalur ini akan diwakili oleh tepi dengan bobot yang lebih besar. Sebuah spanning tree untuk grafik yang akan menjadi bagian dari orang jalan yang tidak memiliki siklus tapi masih terhubung ke setiap rumah. Mungkin ada beberapa kemungkinan pohon merentang.Sebuah pohon rentang minimum akan menjadi satu dengan total biaya terendah.

Kemungkinan multiplisitas


Angka ini menunjukkan mungkin ada lebih dari satu pohon rentang minimum dalam grafik. Dalam gambar tersebut, dua pohon di bawah grafik dua kemungkinan pohon rentang minimum dari grafik yang diberikan.
Mungkin ada beberapa pohon rentang minimum dari berat yang sama memiliki jumlah minimum pinggiran, khususnya, jika semua bobot tepi sebuah grafik yang diberikan adalah sama, maka setiap pohon rentang dari graf yang minimal. Jika ada simpul n dalam grafik, maka pohon masing-masing memiliki n -1 tepi.


Keunikan

Jika ujung masing-masing memiliki berat yang berbeda maka hanya akan ada satu, minimal spanning tree yang unik. Hal ini dapat dibuktikan dengan induksi atau kontradiksi . Hal ini berlaku dalam situasi yang realistis, seperti contoh perusahaan TV kabel di atas, di mana itu tidak mungkin ada dua jalur memiliki biaya yang sama persis. Ini untuk mencakup hutan generalizes juga.
Sebuah bukti keunikan dengan kontradiksi adalah sebagai berikut. [1]
  1. Katakanlah kita memiliki sebuah algoritma yang menemukan suatu MDT (yang akan kita sebut A) berdasarkan struktur grafik dan urutan tepi ketika diperintahkan berat. (Algoritma tersebut memang ada, lihat di bawah.)
  2. Asumsikan MST adalah tidak unik.
  3. Ada lagi spanning tree dengan bobot yang sama, katakanlah MST B.
  4. Misalkan e1 menjadi keunggulan yang di A tapi tidak di B.
  5. Sebagai B merupakan MST, {e1} \ Cangkir B harus mengandung C siklus.
  6. Maka B harus mencakup setidaknya satu e2 ujung yang tidak ada di A dan terletak pada C.
  7. Asumsikan berat e1 adalah kurang dari e2.
  8. Ganti dengan e1 e2 B menghasilkan pohon rentang {e1} \ Cangkir B - {e2} yang memiliki bobot lebih kecil dibandingkan dengan B.
  9. Kontradiksi. Seperti yang kita diasumsikan B adalah MST tapi tidak.
Jika berat e1 lebih besar daripada e2, argumen yang serupa yang melibatkan pohon {e2} \ Cangkir A - {e1} juga menyebabkan kontradiksi. Jadi, kita menyimpulkan bahwa asumsi yang ada dapat menjadi MDT kedua palsu.


Minimum biaya subgraf

Jika bobot yang positif, maka pohon rentang minimum pada kenyataannya minimum biaya- subgraf menghubungkan semua simpul, karena subgraphs mengandung siklus selalu memiliki lebih berat total.


Siklus properti

Untuk setiap C siklus dalam grafik, jika berat e tepi C adalah lebih besar dari bobot tepi lain dari C, maka tepi ini tidak bisa milik sebuah MST. Dengan asumsi sebaliknya , yaitu bahwa e dimiliki oleh T1 MST, maka e menghapus akan pecah menjadi dua sub pohon T1 dengan dua ujung e di sub pohon yang berbeda. Sisa C menghubungkan kembali subpohon, maka ada f tepi C dengan berakhir di subpohon yang berbeda, yaitu, menghubungkan kembali ke sub-pohon T2 pohon dengan berat badan kurang dari itu T1, karena berat dari f kurang dari berat e.


Cut properti


Angka ini menunjukkan properti memotong MSP.T adalah MST dari grafik yang diberikan. Jika S = {A, B, D, E}, sehingga VS = {C, F}, maka ada 3 kemungkinan dari tepi di potong (S, VS), mereka tepi SM, EC, EF asli grafik. Kemudian, e adalah salah satu dari minimum-tepi berat badan-untuk memotong, karena S ∪ {e} adalah bagian dari T. MST
Untuk setiap potong C di grafik, jika berat e tepi C adalah lebih kecil dari bobot tepi lain dari C, maka tepi ini milik semua MSTS grafik. Memang, berasumsi sebaliknya , misalnya, tepi SM (tertimbang 6) milik T MST bukan e tepi (tertimbang 4) pada gambar kiri. Kemudian menambahkan e untuk T akan menghasilkan sebuah siklus, saat mengganti SM dengan e akan menghasilkan MST berat yang lebih kecil.

[ sunting ]Minimum biaya tepi

Jika tepi grafik dengan e biaya minimum adalah unik, maka tepi ini disertakan dalam setiap MST. Memang, jikae tidak termasuk dalam MST, menghapus salah satu (biaya besar) tepi dalam siklus yang terbentuk setelah menambahkan e ke MST, akan menghasilkan pohon rentang berat yang lebih kecil.


Algoritma

Algoritma pertama untuk mencari pohon rentang minimum dikembangkan oleh ilmuwan Ceko Otakar Boruvkapada tahun 1926 (lihat algoritma Boruvka ). Tujuannya adalah cakupan listrik efisien Moravia . Sekarang ada dua algoritma yang umum digunakan, algoritma Prim dan algoritma Kruskal . Ketiga adalah algoritma serakahyang berjalan dalam waktu polinomial, jadi masalah menemukan pohon tersebut adalah di FP , dan terkaitmasalah keputusan seperti menentukan apakah tepi tertentu di MST atau menentukan jika berat total minimal melebihi nilai tertentu sedang P . Lain algoritma greedy tidak umum digunakan adalah algoritma reverse-delete , yang merupakan kebalikan dari algoritma Kruskal.
Jika bobot sisi adalah bilangan bulat, maka algoritma deterministik dikenal yang memecahkan masalah dalamO (m + n) operasi bilangan bulat. [2] Dalam model perbandingan, di mana operasi hanya diperbolehkan pada bobot edge perbandingan berpasangan, Karger, Klein & Tarjan (1995) menemukan waktu linier algoritma acakberdasarkan kombinasi algoritma Boruvka dan algoritma reverse-delete. [3] [4] Apakah masalah dapat diselesaikan deterministik dalam waktu linier dengan algoritma perbandingan berbasis tetap terbuka pertanyaan, namun. Algoritma non-acak tercepat berbasis perbandingan, oleh Bernard Chazelle , didasarkan pada tumpukan yang lembut , sebuah antrian prioritas perkiraan. [5] [6] Its waktu berjalan adalah O (m Î± (m, n)), di mana m adalah jumlah tepi, n adalah jumlah simpul dan α adalah fungsional klasik invers dari fungsi Ackermann .Para α Fungsi tumbuh sangat lambat, sehingga untuk semua tujuan praktis dapat dianggap konstan tidak lebih besar dari 4, dengan demikian algoritma ini membutuhkan Chazelle sangat dekat dengan waktu linier. Seth Pettie dan Vijaya Ramachandran telah menemukan deterministik provably optimal perbandingan minimum berdasarkan rentang algoritma pohon, kompleksitas komputasi yang tidak diketahui. [7]
Penelitian juga dianggap algoritma paralel untuk masalah minimum pohon rentang. Dengan jumlah linier prosesor adalah mungkin untuk memecahkan masalah dalam O (log n) waktu.[8] [9] Bader & Cong (2003) menunjukkan suatu algoritma yang dapat menghitung MSTS 5 kali lebih cepat pada 8 prosesor daripada sekuensial dioptimalkan algoritma. [10] Biasanya, algoritma paralel didasarkan pada algoritma Boruvka-Prim dan Algoritma Kruskal terutama tidak skala juga untuk prosesor tambahan.
Algoritma khusus lainnya telah dirancang untuk komputasi pohon rentang minimum dari graf begitu besar sehingga sebagian besar harus disimpan pada disk setiap saat. Algoritma inipenyimpanan eksternal, misalnya seperti dijelaskan dalam "Teknik sebuah Minimum Spanning Tree Memori Eksternal Algoritma" oleh Roman Dementiev dkk,. [11] dapat beroperasi sesedikit 2 sampai 5 kali lebih lambat daripada tradisional di memori algoritma, mereka mengklaim bahwa "besar masalah pohon rentang minimum yang mengisi beberapa hard disk bisa diselesaikan dalam semalam pada PC." Mereka mengandalkan penyimpanan eksternal yang efisien algoritma pengurutan dan teknik grafik kontraksi untuk mengurangi ukuran grafik secara efisien.
Masalah ini juga dapat didekati dengan cara yang didistribusikan. Jika setiap node dianggap komputer dan node tidak ada yang tahu apa-apa kecuali link sendiri terhubung, kita masih bisa menghitung minimum pohon rentang terdistribusi .


MST pada grafik lengkap

Alan M. dekorasi menunjukkan bahwa diberi grafik lengkap pada n simpul, dengan bobot tepi yang independen variabel acak terdistribusi secara identik dengan fungsi distribusi Fmemuaskan F '(0)> 0, maka sebagai pendekatan n + ∞ berat yang diharapkan dari pendekatan MST Î¶ (3) / F '(0), dimana Î¶ adalah Riemann zeta fungsi . Berdasarkan asumsi tambahan varians terbatas, Alan M. dekorasi juga terbukti konvergensi dalam probabilitas. Selanjutnya, J. Michael Steele menunjukkan bahwa asumsi varians dapat dijatuhkan.
Dalam pekerjaan kemudian, Svante Janson terbukti teorema limit sentral untuk berat badan dari MST.
Untuk bobot acak seragam pada [0,1], ukuran yang diharapkan tepat dari pohon rentang minimum telah dihitung untuk grafik sempurna kecil. [12]
SimpulDiharapkan ukuranApproximative diharapkan ukuran
21 / 20.5
33 / 40.75
431 / 350.8857143
5893 / 9240.9664502
6278 / 2731.0183151
730739 / 291721.053716
8199462271 / 1848483781.0790588
9126510063932 / 1152288530251.0979027


masalah Terkait

Masalah terkait adalah pohon rentang minimum-k (k-MST), yang merupakan pohon yang mencakup beberapa subset dari simpul k dalam grafik dengan berat minimal.
Satu set k-pohon mencakup terkecil adalah bagian dari pohon k mencakup (dari semua pohon merentang mungkin) sehingga tidak ada pohon rentang luar subset memiliki berat yang lebih kecil. [13] [14] [15] (Perhatikan bahwa masalah ini adalah tidak terkait dengan k-pohon merentang minimum.)
The minimum pohon rentang Euclidean adalah pohon rentang dari graf dengan bobot tepi sesuai dengan jarak Euclidean antara titik yang titik-titik dalam pesawat (atau ruang).
Para minimum pohon rentang bujursangkar adalah pohon rentang dari graf dengan bobot tepi sesuai dengan jarak bujursangkar antara simpul yang titik-titik dalam pesawat (atau ruang).
Dalam model terdistribusi , di mana setiap node dianggap komputer dan node tidak ada yang tahu apa-apa kecuali link sendiri terhubung, satu dapat mempertimbangkan pohon rentang minimum didistribusikan . Definisi matematika dari masalah adalah sama tetapi memiliki pendekatan yang berbeda untuk solusi.
Para minimum pohon capacitated rentang adalah pohon yang memiliki simpul ditandai (asal, atau root) dan masing-masing sub-pohon yang melekat pada node berisi tidak lebih dari sebuah node c. c disebut kapasitas pohon. Memecahkan CMST optimal membutuhkan waktu eksponensial, tetapi heuristik yang baik seperti Esau-Williams dan Sharma menghasilkan solusi dekat dengan optimal dalam waktu polinomial.
Para Gelar dibatasi pohon rentang minimum adalah pohon rentang minimum dengan setiap simpul terhubung ke simpul tidak lebih dari yang lain d, untuk beberapa d angka yang diberikan. Kasus ini d = 2 adalah kasus khusus dari masalah salesman keliling , sehingga tingkat dibatasi pohon rentang minimum adalah NP-keras pada umumnya.
Untuk grafik diarahkan , masalah minimum pohon rentang disebut Arborescence masalah dan dapat diselesaikan dalam waktu kuadrat menggunakan algoritma Chu-Liu/Edmonds .
Sebuah pohon rentang maksimum merupakan spanning tree dengan berat badan lebih besar dari atau sama dengan berat dari setiap pohon rentang lain. Seperti pohon dapat ditemukan dengan algoritma seperti Prim atau Kruskal setelah itu mengalikan bobot tepi dengan -1 dan memecahkan masalah MST pada grafik yang baru. Sebuah jalan di pohon rentang maksimum adalah jalan terluas dalam grafik antara dua endpoint:. di antara semua jalur yang mungkin, hal tersebut akan memaksimalkan berat tepi minimum berat badan [16]
Masalah MST dinamis menyangkut update dari MST yang sebelumnya dihitung setelah perubahan berat kelebihan dalam grafik asli atau penyisipan / penghapusan simpul. [17] [18]


hambatan minimum spanning tree

Sebuah hambatan adalah tepi tepi tertimbang tertinggi dalam pohon rentang.
Sebuah pohon rentang adalah pohon rentang minimum hambatan (atau MBST) jika grafik tidak berisi spanning tree dengan berat hambatan yang lebih kecil tepi.
Sebuah MST adalah tentu MBST (dibuktikan dengan properti dipotong ), tetapi MBST adalah belum tentu MST. Jika tepi hambatan dalam MBST adalah jembatan di grafik, maka semua pohon merentang yang MBSTs.

DIJSKTRA
Algoritma Dijkstra, (dinamai menurut penemunya, seorang ilmuwan komputer, Edsger Dijkstra), adalah sebuah algoritma rakus (greedy algorithm) yang dipakai dalam memecahkan permasalahan jarak terpendek (shortest path problem) untuk sebuah graf berarah (directed graph) dengan bobot-bobot sisi (edge weights) yang bernilai tak-negatif.
Misalnya, bila vertices dari sebuah graf melambangkan kota-kota dan bobot sisi (edge weights) melambangkan jarak antara kota-kota tersebut, maka algoritma Dijkstra dapat digunakan untuk menemukan jarak terpendek antara dua kota.
Input algoritma ini adalah sebuah graf berarah yang berbobot (weighted directed graph) G dan sebuah sumber vertex s dalam G dan V adalah himpunan semua vertices dalam graph G.
Setiap sisi dari graf ini adalah pasangan vertices (u,v) yang melambangkan hubungan dari vertex u ke vertex v. Himpunan semua tepi disebutE.
Bobot (weights) dari semua sisi dihitung dengan fungsi
w: E → [0, ∞)
jadi w(u,v) adalah jarak tak-negatif dari vertex u ke vertex v.
Ongkos (cost) dari sebuah sisi dapat dianggap sebagai jarak antara dua vertex, yaitu jumlah jarak semua sisi dalam jalur tersebut. Untuk sepasang vertex s dan t dalam V, algoritma ini menghitung jarak terpendek dari s ke t.

Pseudocode

1  function Dijkstra(G, w, s)
 2     for each vertex v in V[G]                        // Initializations
 3           d[v] := infinity
 4           previous[v] := undefined
 5     d[s] := 0                                        // Distance from s to s
 6     S := empty set
 7     Q := V[G]                                        // Set of all vertices
 8     while Q is not an empty set                      // The algorithm itself
 9           u := Extract_Min(Q)
10           S := S union {u}
11           for each edge (u,v) outgoing from u
12                  if d[u] + w(u,v) < d[v]             // Relax (u,v)
13                        d[v] := d[u] + w(u,v) 
14                        previous[v] := u





Comments

Post a Comment